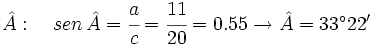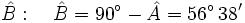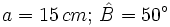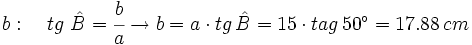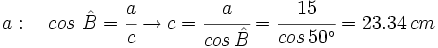Se denomina al triángulo rectángulo en el que uno de sus ángulos es recto, es decir, mide 90° (grados sexagesimales) ó π/2 radianes.
Visitar esta pag:
http://mediateca.educa.madrid.org/reproducir.php?id_video=fn274mhbnxx8eyso
TEOREMA DE PITAGORAS
Vamos a comprobar que eso es cierto supoerponiendo las áreas.
Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.
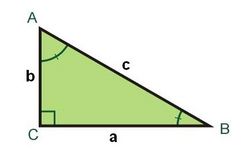
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.
Ejemplos: Resolución de triángulos rectángulos
visitar estas paginas: Las MaTICS en 6to grado
Aerazo.blogspot
Visitar esta pag:
http://mediateca.educa.madrid.org/reproducir.php?id_video=fn274mhbnxx8eyso
TEOREMA DE PITAGORAS
El teorema de Pitágoras dice que en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, c2=a2+b2.
Geométricamente se traduce en que el área del cuadrado de lado la hipotenusa es igual a la suma de las áreas de los cuadrados de lados los catetos.Vamos a comprobar que eso es cierto supoerponiendo las áreas.
Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.
 | 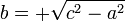 |  |
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.
Ejemplos: Resolución de triángulos rectángulos
- Caso 1: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 11 cm y la hipotenusa que mide 20 cm.
- Caso 2: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 15 cm y su ángulo contiguo que mide 50º.
visitar estas paginas: Las MaTICS en 6to grado
Aerazo.blogspot

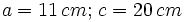
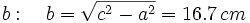 (Por el
(Por el