El mundo de las matematicas
BIENVENIDOSEste blog se crea para que el estudiante se apoye en los conceptos básicos de las matematicas y realice algunos ejercicios de manera práctica
lunes, 25 de junio de 2012
domingo, 24 de junio de 2012
jueves, 3 de mayo de 2012
HISTORIA DE LA TRIGONOMETRIA
Los antiguos egipcios y los babilonios
conocían ya los teoremas sobre las proporciones de los lados de los triángulos
semejantes. Pero las sociedades pre-helénica carecían de la noción de una
medida del ángulo y por lo tanto, los lados de los triángulos se estudiaron en
su medida, un campo que se podría llamar trilaterometría.
Los astrónomos babilonios llevaron
registros detallados sobre la salida y puesta de las estrellas, el movimiento
de los planetas y los eclipses solares y lunares, todo lo cual requiere la
familiaridad con la distancia angular medida sobre la esfera celeste. Sobre la
base de una interpretación de la tablilla cuneiforme Plimpton 322 (c. 1900 aC), algunos incluso han afirmado que los antiguos babilonios
tenían una tabla de secantes. Hoy, sin embargo, hay un gran debate acerca de si
se trata de una tabla de ternas pitagóricas, una tabla de soluciones de
ecuaciones segundo grado, o una tabla trigonométrica.
Papiro de Ahmes
Los egipcios, en el segundo milenio antes
de Cristo, utilizaban una forma primitiva de la trigonometría, para la
construcción de las pirámides. El Papiro de Ahmes, escrito por el escriba egipcio Ahmes (c.
1680-1620 aC), contiene el siguiente problema relacionado con la trigonometría:
"Si una pirámide es de 250 codos de
alto y al lado de su base de 360 codos de largo, ¿cuál es su Seked?"
La solución, al
problema, es la relación entre la mitad del lado de la base de la pirámide a su
altura. En otras palabras, la cantidad que encontró para la seked es la cotangente del ángulo que forman la base de la
pirámide y su cara.
MEDIDA ANGULAR
En la medición de ángulos, y por tanto en trigonometría, se emplean tres
unidades, si bien la más utilizada en la vida cotidiana es el Grado
sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la
unidad natural para medir ángulos, el Grado centesimal se desarrolló como la
unidad más próxima al sistema decimal,
se usa en topografía, arquitectura o en construcción.
§ Radián: unidad angular natural en trigonometría, será la que
aquí utilicemos. En una circunferencia completa hay 2π radianes.
§ Grado sexagesimal: unidad angular que divide una
circunferencia en 360 grados.
§ Grado centesimal: unidad angular que divide la circunferencia
en 400 grados centesimales.
viernes, 11 de noviembre de 2011
TRIANGULOS RECTANGULO Y TEOREMA DE PITAGORAS
Se denomina al triángulo rectángulo en el que uno de sus ángulos es recto, es decir, mide 90° (grados sexagesimales) ó π/2 radianes.
Visitar esta pag:
http://mediateca.educa.madrid.org/reproducir.php?id_video=fn274mhbnxx8eyso
TEOREMA DE PITAGORAS
Vamos a comprobar que eso es cierto supoerponiendo las áreas.
Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.
Ejemplos: Resolución de triángulos rectángulos
visitar estas paginas: Las MaTICS en 6to grado
Aerazo.blogspot
Visitar esta pag:
http://mediateca.educa.madrid.org/reproducir.php?id_video=fn274mhbnxx8eyso
TEOREMA DE PITAGORAS
El teorema de Pitágoras dice que en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, c2=a2+b2.
Geométricamente se traduce en que el área del cuadrado de lado la hipotenusa es igual a la suma de las áreas de los cuadrados de lados los catetos.Vamos a comprobar que eso es cierto supoerponiendo las áreas.
Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.
 | 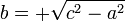 |  |
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.
Ejemplos: Resolución de triángulos rectángulos
- Caso 1: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 11 cm y la hipotenusa que mide 20 cm.
- Caso 2: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 15 cm y su ángulo contiguo que mide 50º.
Solución:[Ocultar]
- Caso 1:
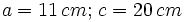
- Hallamos el cateto
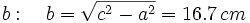 (Por el teorema de Pitágoras)
(Por el teorema de Pitágoras) - El ángulo
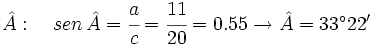
- Hallamos el ángulo
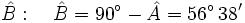
- Caso 2:
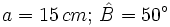
- Hallamos el cateto
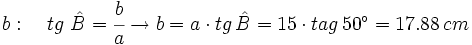
- Hallamos el cateto
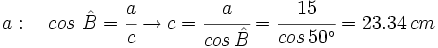
visitar estas paginas: Las MaTICS en 6to grado
Aerazo.blogspot
Suscribirse a:
Comentarios (Atom)